Implementing 2-3 trees

Today I show how I have implemented 2-3 trees in a straightforward way.

I consider 2-3 trees to be perhaps the simplest possible kind of balanced search tree data structure. At least conceptually.

A while ago I showed how to implement AVL trees in not too many lines of code. However, I had to be very careful, and there was one weird special case that I had to make sure to handle appropriately to avoid getting in an infinite loop.

The code for 2-3 trees is, I think, simpler. It’s not necessarily shorter, but it’s more straightforward. There are no exceptional cases to handle, there are no tree rotations, etc. Just an intuitive recursive implementation of each operation.

What are 2-3 trees

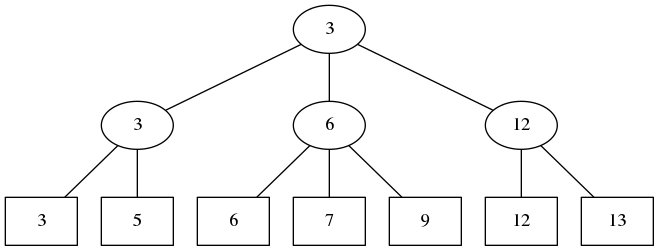
2-3 trees are a kind of balanced search tree. They have, in this implementation, the following properties:

• Every internal node has 2 or 3 children.
• All leaves are always at the same depth.
• The above guarantees that the height is $\Theta(\log n)$.
• All keys are stored in the leaves. This makes it simpler, since we can just discard and create internal nodes at will.
• Internal nodes store the height of the subtree, and the smallest element of the subtree.
• The tree is ordered. For a node with two children, the left subtree contains elements less than or equal to the right subtree. For a node with three children, the left subtree contains elements less than or equal to the middle subtree, and the middle subtree contains elements less than or equal to the right subtree.

Define the data type

Let’s start implementing this in Haskell.

The data type Tree t is the type of 2-3 trees containing elements of type t.

A tree is either empty, or it is a leaf, or it starts with an internal node at the root. We make separate constructors for 2-children nodes and 3-children nodes.

data Tree t =
    Empty
  | Leaf t
  | Node2 Int t (Tree t) (Tree t)          -- Node2 height smallest a b
  | Node3 Int t (Tree t) (Tree t) (Tree t) -- Node3 height smallest a b c

Also define a couple helper functions to extract the height and the smallest element of a tree. The height of a leaf is 0.

height :: Tree t -> Int
height (Leaf _) = 0
height (Node2 h _ _ _) = h
height (Node3 h _ _ _ _) = h

smallest :: Tree t -> t
smallest (Leaf x) = x
smallest (Node2 _ s _ _) = s
smallest (Node3 _ s _ _ _) = s

Now a couple functions for building 2-nodes and 3-nodes out of subtrees, which are assumed to be of equal height. These functions calculate the height and the smallest element from the left-most child.

node2 :: Tree t -> Tree t -> Tree t
node2 a b = Node2 (height a + 1) (smallest a) a b

node3 :: Tree t -> Tree t -> Tree t -> Tree t
node3 a b c = Node3 (height a + 1) (smallest a) a b c

Merging trees

Our basic operation is merge. It takes two trees, where all elements in one are no larger than all elements in the other, and creates one tree that contains their union. Every other operation will be defined in terms of merge.

The following helper function will be useful: take between 2 and 4 trees of the same height, containing elements in sorted order (i.e. the first tree contains the smallest elements, etc), and “level up”, creating between 1 and 2 trees of height one larger.

For 2 or 3 subtrees we end up with one tree, for 4 subtrees we end up with 2 trees.

levelUp :: [Tree t] -> [Tree t]
levelUp [a,b] = [node2 a b]
levelUp [a,b,c] = [node3 a b c]
levelUp [a,b,c,d] = [node2 a b, node2 c d]

Next comes the recursive helper function, mergeToSameHeight. Given two non-empty trees to merge, it returns either 1 or 2 trees. The height of the output(s) is always equal to the maximum of the heights of the inputs.

If the two inputs are already same height, we just return them.

If the first tree is smaller, we merge it with the left-most subtree of the second tree, which generates either 1 or 2 subtrees to replace that left-most subtree. So we get between 2 and 4 subtrees, and we “level up” to get the output(s).

Similarly, if the second tree is smaller, we merge it with the right-most subtree of the first tree, and “level up”.

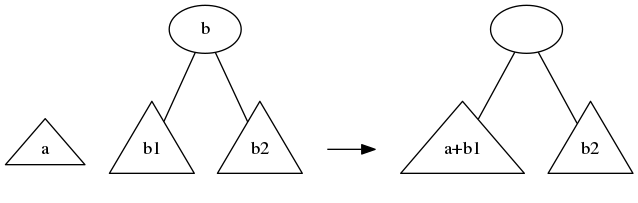
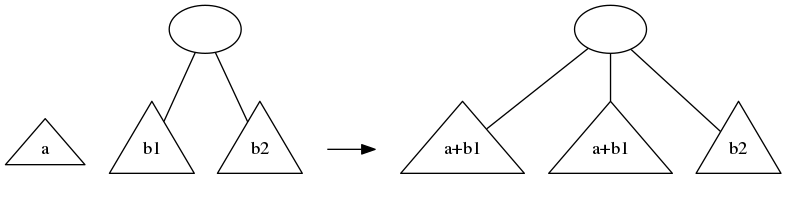
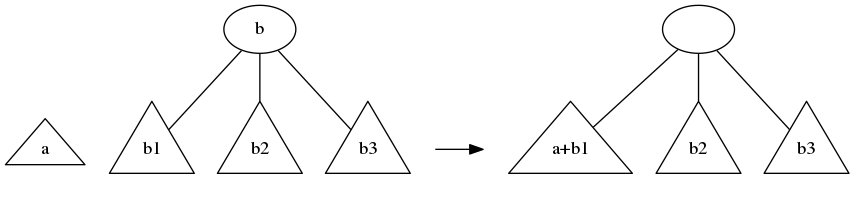
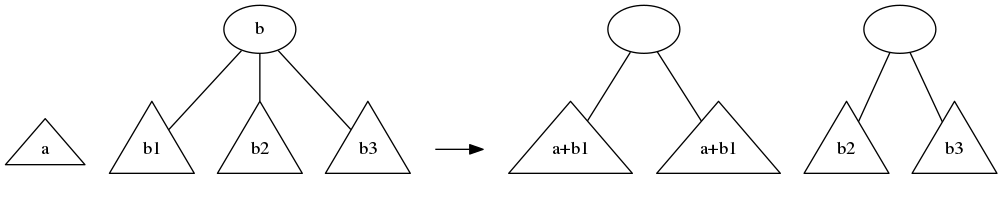
mergeToSameHeight :: Tree t -> Tree t -> [Tree t]
mergeToSameHeight a b
  | height a < height b =
    case b of
      Node2 _ _ b1 b2 -> levelUp (mergeToSameHeight a b1 ++ [b2])
      Node3 _ _ b1 b2 b3 -> levelUp (mergeToSameHeight a b1 ++ [b2, b3])
  | height a > height b =
    case a of
      Node2 _ _ a1 a2 -> levelUp ([a1] ++ mergeToSameHeight a2 b)
      Node3 _ _ a1 a2 a3 -> levelUp ([a1,a2] ++ mergeToSameHeight a3 b)
  | otherwise = [a, b]

merge just calls mergeToSameHeight. If two trees are generated at the top level, we add an extra level at the top. This is how 2-3 trees grow: they grow at the root!

merge :: Tree t -> Tree t -> Tree t

merge a Empty = a
merge Empty b = b

merge a b =
  case mergeToSameHeight a b of
    [t] -> t
    [t, u] -> node2 t u

The run time of merge is proportional to the difference of heights of the inputs.

Splitting trees

We define the split operation that takes a function to split the elements by (e.g. “all elements larger than 5 go to the right”) and a tree, and returns two trees. The function f returns True if the element should go to the right, and False if it should go to the left.

By looking at the smallest element in each subtree, we can figure out which subtree needs to be split. Then we use merge to merge the pieces of the subtree with the other subtrees.

split :: (t -> Bool) -> Tree t -> (Tree t, Tree t)

split _ Empty = (Empty, Empty)

split f (Leaf x)
  | f x   = (Empty, Leaf x)
  | otherwise  = (Leaf x, Empty)

split f (Node2 _ _ a b)
  | f (smallest b) =
    let (a1,a2) = split f a in (a1, merge a2 b)
  | otherwise =
    let (b1,b2) = split f b in (merge a b1, b2)

split f (Node3 _ _ a b c)
  | f (smallest b) =
    let (a1,a2) = split f a in (a1, merge a2 (node2 b c))
  | f (smallest c) =
    let (b1,b2) = split f b in (merge a b1, merge b2 c)
  | otherwise =
    let (c1,c2) = split f c in (merge (node2 a b) c1, c2)

The runtime of split is $O(\log n)$. All the merging going on starts from small trees and works its way up to larger and larger trees. Because the time to merge only depends on the difference of heights, the total time adds up to the height of the tree, which is $O(\log n)$.

Contains, insert, delete

These functions are now easy. We just split the tree around the element we are interested in, do the operation we want, and merge things back as appropriate.

contains :: Ord t => Tree t -> t -> Bool
contains a x =
  case split (>= x) a of
    (_, Empty) -> False
    (_, a2) -> smallest a2 == x

insert :: Ord t => Tree t -> t -> Tree t
insert a x =
  let (a1, a2) = split (>= x) a
  in a1 `merge` (Leaf x) `merge` a2

delete :: Ord t => Tree t -> t -> Tree t
delete a x =
  let (a1, a2) = split (>= x) a
      (_, a3) = split (>x) a2
  in merge a1 a3

Converting from and to lists

Just to make it easier to create trees and inspect trees, we add conversion functions to and from lists.

To create a tree from an unsorted list of elements, just insert all the elements starting from an empty tree.

fromList :: Ord t => [t] -> Tree t
fromList = foldl insert Empty

To convert to a list, we could recursively convert subtrees to lists and merge. But that would be $\Theta(n \log n)$. We can do it better, in $\Theta(n)$, by creating a helper function that prepends all the elements in front of a list. This way we don’t have to merge lists.

prepend :: Tree t -> [t] -> [t]
prepend Empty xs = xs
prepend (Leaf x) xs = x : xs
prepend (Node2 _ _ a b) xs = prepend a (prepend b xs)
prepend (Node3 _ _ a b c) xs = prepend a (prepend b (prepend c xs))

toList :: Tree t -> [t]
toList a = prepend a []

That’s all the basic operations. If you need more, they should be easy to add. It works, I’ve tested it.