Balanced binary search trees: the easy way

The task of balancing binary search trees has a reputation of being very hard to implement. Data structure books usually list dozens of different cases, especially for deleting elements.

Let’s change this - it’s not that hard! The analysis will be a little involved, but the code is going to be simple.

Here are some design choices:

• We’ll implement AVL trees. These are binary trees where two sibling subtrees have heights differing by at most 1. This guarantees $\Theta(\log n)$ depth.
• All elements are stored in the leaves. This is unusual, people usually store values in internal nodes. But it makes things so much simpler!
• Internal nodes store a reference to the smallest (left-most) element of the sub-tree. This will be useful to guide us down the tree.
• Internal nodes also store the sub-tree height. AVL trees are usually described with nodes only storing the height difference of their children, but storing the height instead makes things easier still.
• We’ll implement this in Haskell. We like algebraic data types for trees!

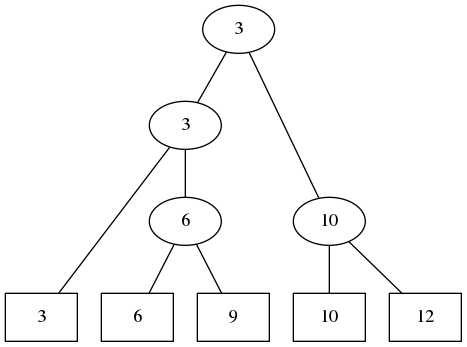
OK, let’s get down to it!

Preliminaries

Start by defining binary trees.

data Tree t = Empty | Leaf t | Node Int t (Tree t) (Tree t)

A tree of elements of type t is either empty, it is a leaf, or it is an internal node. A leaf contains a value of type t. An internal node contains: the height, the smallest element in the sub-tree, and the two children.

Let’s add some helper functions:

height :: Tree t -> Int
height Empty = error "height Empty"
height (Leaf _) = 0
height (Node h _ _ _) = h

smallest :: Tree t -> t
smallest Empty = error "smallest Empty"
smallest (Leaf x) = x
smallest (Node _ s _ _) = s

left, right :: Tree t -> Tree t
left  (Node _ _ a _) = a
left _ = error "only internal nodes have children"
right (Node _ _ _ b) = b
right _ = error "only internal nodes have children"

toList :: Tree t -> [t]
toList Empty = []
toList (Leaf x) = [x]
toList (Node _ _ a b) = toList a ++ toList b

The toList function is not optimal: it works in $\Theta(n \log n)$ time (why?). $\Theta(n)$ is possible. I’ll leave that as a coding exercise.

Time for some AVL-specific stuff. How do we build and balance trees? As a reminder, this is how AVL trees work:

• All elements in the left sub-tree should be smaller (or equal) to all the elements in the right sub-tree.
• The difference in height of the two sub-trees should be at most 1. We call this “similar height”.

Let’s create another little helper function: build a tree from two sub-trees of similar height:

node :: Tree t -> Tree t -> Tree t
node a b
  | abs (height a - height b) <= 1
    = Node (max (height a) (height b) + 1) (smallest a) a b
  | otherwise = error "unbalanced tree"

It’s finally time to start really manipulating our trees:

Merging trees

Wait, what? Merging trees as the first operation? What about insert?

We’ll get to insert later. As you’ll see, merge is going to be our basic operation. Everything else will be defined in terms of it!

What do we mean by merge? Suppose we have two trees, A and B, such that all elements of A are smaller or equal to all elements of B. The merged tree will contain all elements from both.

The node operation works when the two trees have similar heights. What if their heights differ by more than 1? Assume that A is the shallower tree and B is the deeper tree.

So B has height $h$ and A has height at most $h-2$. Our strategy is going to be as follows: merge A with left B, then merge the resulting tree with right B. Does this work?

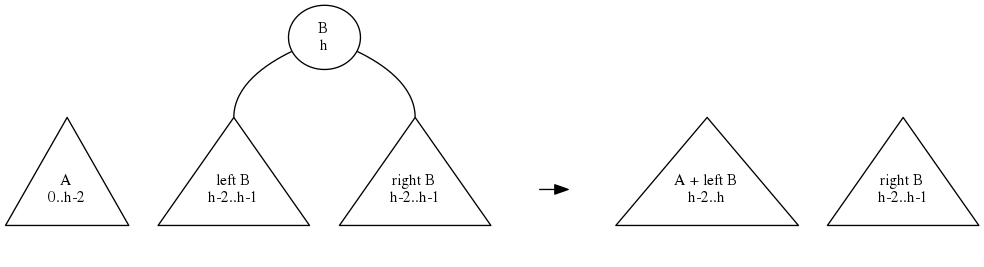
Above image shows what happens after the first step: merging A with the left child of B. Each node shows possible heights.

The merge of trees of heights $h_1$ and $h_2$ is always going to be a tree of height either $\max(h_1, h_2)$ or $\max(h_1,h_2)+1$. This will be easy to verify once we have the whole merging algorithm.

OK, so what exactly happened when we tried to merge two trees with non-similar heights? After merging the smaller tree with one of the subtrees, we again have two trees to merge.

In many cases, the resulting trees already are of similar height. In that case, a call to node will finish the job.

But it is possible that we get a height difference of 2. This may only happen if the left subtree of B is deeper than the right subtree of B, and merging the left subtree of B with A further increases its height.

At least we’re close! We now want to recursively merge these two trees using the same method. Will that work?

So we use the same method as above. Sometimes it will result in trees of similar height, and again we are done.

But it is possible that we run into the “bad” case again, where the “middle” subtree is the largest one. This is how it will look like:

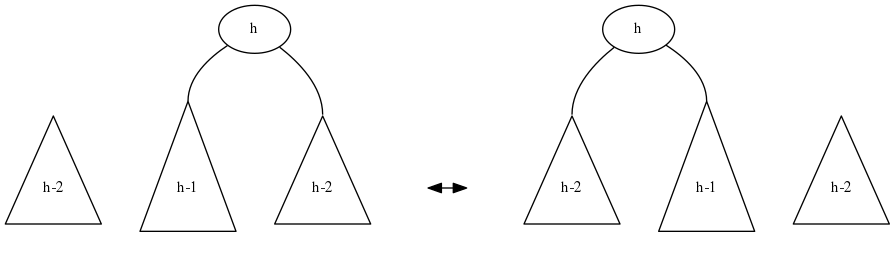
Uh oh! We get into an infinite loop, going back and forth between the two mirror image cases!

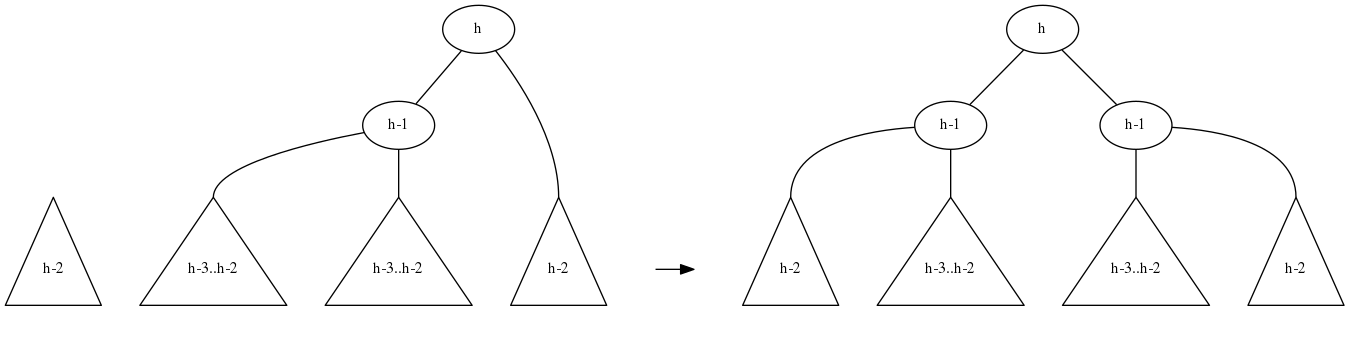
We need to use a different strategy in this special case, to break the cycle. Fortunately, it’s easy: we have four subtrees of similar heights, just pair them up:

Merge code

merge :: Tree t -> Tree t -> Tree t
merge Empty x = x
merge x Empty = x
merge a b
  | abs (height a - height b) <= 1
    = node a b
  | height a == height b - 2 && height (right b) == height b - 2
    -- the special case: [h-2] + {[h-1],[h-2]}
    = let (bl,br) = (left b, right b)
          (bll,blr) = (left bl, right bl)
      in node (node a bll) (node blr br)
  | height a < height b
    = merge (merge a (left b)) (right b)
  | otherwise
    = merge (left a) (merge (right a) b)

That’s it! Pretty short, huh? That’s all we need.

How long does a merge take? We always reduce the difference in heights in the first recursive call, and finish by merging two trees of heights differing by at most 2, which takes constant time. Therefore, merging two trees of heights $h_1$ and $h_2$ takes $\Theta(|h_1 - h_2| + 1)$ time.

Splitting trees

Now we want to do the reverse of merging: split a tree into two smaller trees. OK but split where? We need some way of telling which elements belong to the left part and which elements belong to the right part.

This is accomplished by a functional argument: a function that returns False for the left elements and True for the right elements. The requirement is that the function be monotonic: we can’t have x < y and x belonging to the right while y belongs to the left. Other than that, any function will do.

You’d think that splitting is going to be more complicated than merging. But no! It’s going to be simpler. In fact, we will use merging to do splitting!

Here is where having the reference to the smallest element of a sub-tree comes in handy:

• If the smallest element of the right sub-tree belongs to the left, the whole left sub-tree belongs to the left, and we only need to split the right sub-tree.
• If the smallest element of the right sub-tree belongs to the right, the whole right sub-tree belongs to the right, and we only need to split the left sub-tree.

split :: Tree t -> (t->Bool) -> (Tree t, Tree t)
split Empty _ = (Empty, Empty)
split (Leaf x) isBig
  | isBig x   = (Empty, Leaf x)
  | otherwise = (Leaf x, Empty)

split (Node _ _ a b) isBig
  | isBig (smallest b)
    = let (a1,a2) = split a isBig
      in (a1, merge a2 b)
  | otherwise
    = let (b1,b2) = split b isBig
      in (merge a b1, b2)

Done.

How fast is it? Since each merge can take $\Theta(\log n)$ time, are we running the risk of having split run in $\Theta(\log^2 n)$ time?

Fortunately, not. Since the cost of merge is proportional to the difference of heights of the two trees we’re merging, and we’re merging deeper and deeper trees, one can prove that the total cost of split is proportional to the height of the full tree.

So we get time $\Theta(\log n)$ for split as well.

Insert, delete, etc

Now that we have split and merge, we can do anything we want, easily! For instance, to insert an element, split he tree around that value, create a third single-element tree, and merge the three trees.

contains :: Ord t => Tree t -> t -> Bool
contains a x =
  case split a (>=x) of
    (_, Empty) -> False
    (_, b) -> smallest b == x

insert :: Ord t => Tree t -> t -> Tree t
insert a x =
  let (a1, a2) = split a (>=x)
  in merge a1 (merge (Leaf x) a2)

delete :: Ord t => Tree t -> t -> Tree t
delete a x =
  let (b, _) = split a (>=x)
      (_, c) = split a (>x)
  in merge b c

fromList :: Ord t => [t] -> Tree t
fromList = foldl insert Empty

Let’s see if it works

$ ghci Tree.hs
GHCi, version 7.4.1: http://www.haskell.org/ghc/  :? for help
Loading package ghc-prim ... linking ... done.
Loading package integer-gmp ... linking ... done.
Loading package base ... linking ... done.
[1 of 1] Compiling Tree             ( Tree.hs, interpreted )
Ok, modules loaded: Tree.
*Tree> let a = fromList [10, 5, 7, 18, 3]
*Tree> toList a
[3,5,7,10,18]
*Tree> toList (insert a 4)
[3,4,5,7,10,18]
*Tree> toList (delete a 10)
[3,5,7,18]
*Tree> contains a 12
False
*Tree> contains a 5
True
*Tree> let (b,c) = split a (\x -> x*x > 50)
*Tree> toList b
[3,5,7]
*Tree> toList c
[10,18]

Yay!